Dijkstra's Algorithm | Single-Source Shortest Path
Dijkstra’s algorithm finds shortest paths from the source vertex to all vertices in the graph. The condition for the algorithm is that all edge weights should be non-negative. Thus, Dijkstra’s algorithm is efficient than the Bellman-Ford algorithm because it processes each edge only once, since it knows that there are no negative-weight edges in the graph.
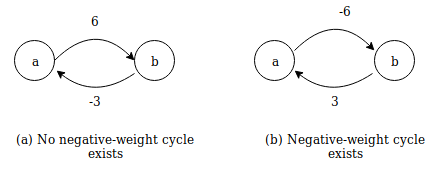
In fig. (a) there is no negative-weight cycle, fig. (b) contains a negative-weight cycle
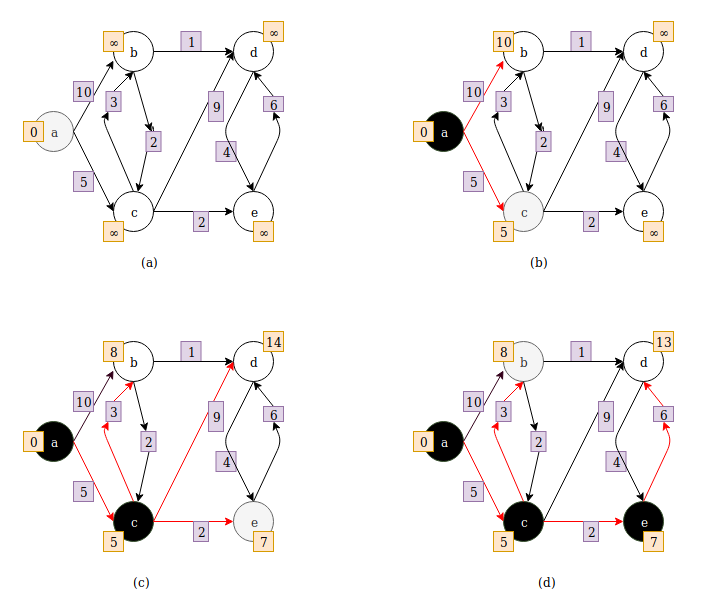
Here the source vertex is a. When the vertex is selected it becomes gray and when it is processed it becomes black.
In fig. (a) vertex a is selected and after it is processed there are two edges to choose, one with weight 10 and one with weight 5.
In fig. (b) edge with weight 5 is selected because the weight is smaller than other edge weight and vertex c is selected. The shortest distance from the source vertex is also update at each vertex.
In fig, (c) distance to vertex e is 7 from source vertex and to vertex d it is 14 from source vertex. After vertex e is processed in fig. (d) the distance to vertex d is 13 from source vertex.
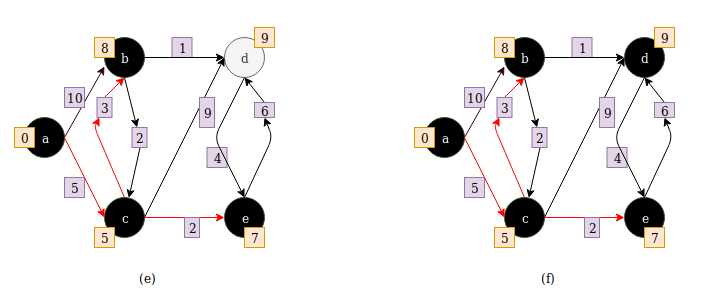
In fig. (f) all vertices are processed and their shortest distance from source vertex is updated.
At each step, Dijkstra’s algorithm selects a vertex that has not been processed yet and whose distance is as small as possible. We can say that it uses a greedy strategy.
To store color, distance of a vertex a data structure is needed. An array is needed to store processed vertices and a minimum priority queue to store unprocessed vertices.
Here is the implementation of dijkstra and relax function.
enum Color {WHITE, BLACK};
struct Vertex
{
std::size_t id;
int distance = std::numeric_limits<int>::max();
Color color = WHITE;
Vertex(std::size_t id) : id(id) {}
};
void relax(std::size_t src, std::size_t dest, int weight)
{
auto& next_dist = vertices[dest].distance;
const auto curr_dist = vertices[src].distance + weight;
if (curr_dist < next_dist)
{
next_dist = curr_dist;
//update distance in unprocessed queue
unprocessed.push( std::make_pair(next_dist, dest));
}
}
void dijkstra(std::size_t src)
{
//initialize distance of source
vertices[src].distance = 0;
unprocessed.push( std::make_pair(vertices[src].distance, src) );
while (!unprocessed.empty())
{
int curr_vertex_dist = unprocessed.top().first;
std::size_t curr_vertex = unprocessed.top().second;
unprocessed.pop();
if (vertices[curr_vertex].color == WHITE)
{
processed.push_back(curr_vertex);
}
vertices[curr_vertex].color = BLACK;
for (auto& ver: adj_list[curr_vertex])
{
relax(curr_vertex, ver.first, ver.second);
}
}
}
relax function updates the distance of the destination vertex and if the new calculated distance is smaller than the stored distance, then the distance is updated and the vertex is pushed in the minimum priority queue.
In the function dijkstra source vertex in passed as an argument. Variable curr_vertex stores the vertex that is nearer to the source because in minimum priority queue element having minimum value is at the top of queue. If the color of the selected vertex is white, then it is pushed into the processed array and then its color changes to black. Then all the vertices that are reachable from the selected vertex are processed.
Here is the C++ implementation of Dijkstra’s Algorithm.
To push vertices in a std::vector, we have used emplace_back instead of push_back.
For emplace_back constructor A (int x_arg) will be called.
And for push_back A (int x_arg) is called first and move A (A &&rhs) is called afterwards. push_back vs emplace_back
Related: Bellman Ford Algorithm
#include <iostream>
#include <vector>
#include <map>
#include <limits>
#include <list>
#include <queue>
class Graph
{
enum Color {WHITE, BLACK};
struct Vertex
{
std::size_t id;
int distance = std::numeric_limits<int>::max();
Color color = WHITE;
Vertex(std::size_t id) : id(id) {}
};
using pair_ = std::pair<std::size_t, int>;
std::vector<Vertex> vertices = {};
//to store processed vertex
std::vector<std::size_t> processed = {};
//adjacency list , store src, dest, and weight
std::vector< std::vector< pair_> > adj_list;
//to store unprocessed vertex min-priority queue
std::priority_queue< pair_, std::vector<pair_>,
std::greater<pair_> > unprocessed;
public:
Graph(std::size_t size);
void add_edge(std::size_t src, std::size_t dest, int weight);
void dijkstra(std::size_t src);
std::ostream& print_distance(std::ostream&) const;
private:
void relax(std::size_t src, std::size_t dest, int weight);
};
Graph::Graph(std::size_t size)
{
vertices.reserve(size);
adj_list.resize(size);
for (int i = 0; i < size; i++)
{
vertices.emplace_back(i);
}
}
void Graph::add_edge(std::size_t src , std::size_t dest, int weight)
{
if(weight >= 0)
{
if (src == dest)
{
throw std::logic_error("Source and destination vertices are same");
}
if (src < 0 || vertices.size() <= src)
{
throw std::out_of_range("Enter correct source vertex");
}
if (dest < 0 || vertices.size() <= dest)
{
throw std::out_of_range("Enter correct destination vertex");
}
int flag = 0, i = src;
for (auto& it : adj_list[i])
{
if (it.first == dest)
{
flag = 1;
break;
}
}
if (flag == 0)
{
adj_list[src].push_back( {dest, weight} );
}
else
{
throw std::logic_error("Existing edge");
}
}
else
{
std::cerr << "Negative weight\n";
}
}
void Graph::relax(std::size_t src, std::size_t dest, int weight)
{
auto& next_dist = vertices[dest].distance;
const auto curr_dist = vertices[src].distance + weight;
if (curr_dist < next_dist)
{
next_dist = curr_dist;
//update distance in unprocessed queue
unprocessed.push( std::make_pair(next_dist, dest));
}
}
void Graph::dijkstra(std::size_t src)
{
//initialize distance of source
vertices[src].distance = 0;
unprocessed.push( std::make_pair(vertices[src].distance, src) );
while (!unprocessed.empty())
{
int curr_vertex_dist = unprocessed.top().first;
std::size_t curr_vertex = unprocessed.top().second;
unprocessed.pop();
if (vertices[curr_vertex].color == WHITE)
{
processed.push_back(curr_vertex);
}
vertices[curr_vertex].color = BLACK;
for (auto& ver: adj_list[curr_vertex])
{
relax(curr_vertex, ver.first, ver.second);
}
}
}
std::ostream& Graph::print_distance(std::ostream& os) const
{
os << "Vertex\t\tDistance from Source\n";
for (auto vertex: vertices)
{
os << vertex.id << "\t\t" << vertex.distance << "\n";
}
return os;
}
int main()
{
Graph grp(5);
grp.add_edge(0, 1, 10);
grp.add_edge(0, 2, 5);
grp.add_edge(1, 3, 1);
grp.add_edge(1, 2, 2);
grp.add_edge(2, 1, 3);
grp.add_edge(2, 3, 9);
grp.add_edge(2, 4, 2);
grp.add_edge(3, 4, 4);
grp.add_edge(4, 3, 6);
grp.add_edge(4, 0, 7);
grp.dijkstra(0);
grp.print_distance(std::cout);
}
View this code on Github
Output

Reference: Introduction to Algorithms The Algorithm Design Manual Data Structures and Algorithms Made Easy Competitive Programmer’s Handbook - Antti Laaksonen