How to find the Length of Loop in Linked List | C++ Implementation

Publish date: 2018-01-20
Tags: Cpp, Algorithm, Linked-List, Data-Structure

Given a Linked List, we have to find does loop exist in Linked List and if yes, find the length of loop.

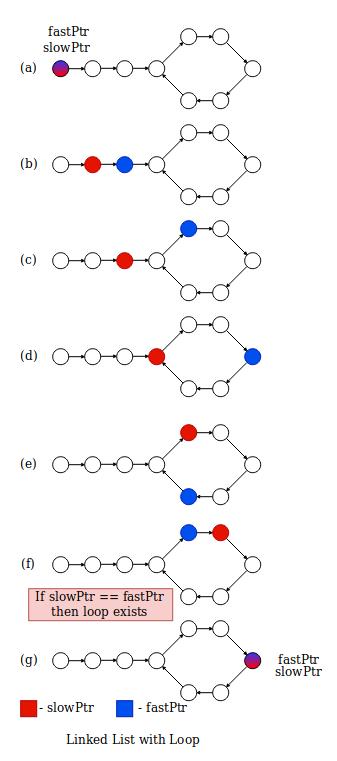
Floyd Cycle Finding Algorithm

To find loop in the linked list, we need two node pointers slowPtr and fastPtr which starts from the head. slowPtr increments by one node while fastPtr increments by two nodes. If these pointers point at the same node after starting from head then loop exists. This algorithm is known as Floyd Cycle Finding Algorithm.

Node* doesLoopExist()
{
    Node *slowPtr = head;
    Node *fastPtr = head;

    while(slowPtr && fastPtr && fastPtr->next)
    {
        slowPtr = slowPtr->next;
        fastPtr = fastPtr->next->next;

        if(slowPtr == fastPtr)
        {
            return slowPtr;
        }
    }
    return nullptr;
}

If loop exists then this function returns node which is pointed by slowPtr and fastPtr and if node doesn’t exist then it returns nullptr.

To calculate length of loop, fastPtr start from its current node and count number of nodes until slowPtr is equal to fastPtr.

int lengthOfLoop()
{
    int count = 0;
    bool loopExist = false;
    Node *slowPtr = nullptr, *fastPtr = nullptr;

    slowPtr = doesLoopExist();
    fastPtr = slowPtr;
    if(slowPtr != nullptr)
    {
        loopExist = true;
    }
    else
    {
        return 0;
    }
    if(loopExist)
    {
        fastPtr = fastPtr->next;
        count++;
        while(slowPtr != fastPtr)
        {
            fastPtr = fastPtr->next;
            count++;
        }
        return count;
    }
    return 0;
}

#include <iostream>
#include <utility>

template <class T>
class LinkedList
{
    struct Node
    {
        T data;
        Node * next;
        Node(T value) : data(std::move(value)), next(nullptr) {}
    };
    Node *head;

  public:
    LinkedList() : head(nullptr) {}
    LinkedList(const LinkedList& ll) = delete; //copy constructor
    LinkedList& operator=(const LinkedList& ll) = delete; //copy assignment
    ~LinkedList();
    void insert(T);
    void createLoop(int);
    int lengthOfLoop();
    Node* doesLoopExist()
    {
        Node *slowPtr = head;
        Node *fastPtr = head;

        while(slowPtr && fastPtr && fastPtr->next)
        {
            slowPtr = slowPtr->next;
            fastPtr = fastPtr->next->next;

            if(slowPtr == fastPtr)
            {
                return slowPtr;
            }
        }
        return nullptr;
    }
};

template <class T>
void LinkedList<T>::insert(T data)
{
    Node *node = new Node(std::move(data));
    Node *tmp = head;
    if(tmp == nullptr)
    {
        head = node;
    }
    else
    {
        while(tmp->next != nullptr)
        {
            tmp = tmp->next;
        }
        tmp->next = node;
    }
}

template <class T>
void LinkedList<T>::createLoop(int n)
{
    Node *tmp = head;
    Node *tail = head;
    for(int i = 0; i < n-1; i++)
    {
        tmp = tmp->next;
    }

    while(tail->next != nullptr)
    {
        tail = tail->next;
    }
    tail->next = tmp;
}

template <class T>
int LinkedList<T>::lengthOfLoop()
{
    int count = 0;
    bool loopExist = false;
    Node *slowPtr = nullptr, *fastPtr = nullptr;

    slowPtr = doesLoopExist();
    fastPtr = slowPtr;
    if(slowPtr != nullptr)
    {
        loopExist = true;
    }
    else
    {
        return 0;
    }
    if(loopExist)
    {
        fastPtr = fastPtr->next;
        count++;
        while(slowPtr != fastPtr)
        {
            fastPtr = fastPtr->next;
            count++;
        }
        return count;
    }
    return 0;
}

template <class T>
LinkedList<T>::~LinkedList()
{
    Node *tmp = nullptr;
    while(head)
    {
        tmp = head;
        head = head->next;
        delete tmp;
    }
    head = nullptr;
}

int main()
{
    LinkedList<char> ll1;
    ll1.insert('p');
    ll1.insert('r');
    ll1.insert('o');
    ll1.insert('g');
    ll1.insert('r');
    ll1.insert('a');
    ll1.insert('m');
    ll1.insert('m');
    ll1.insert('e');
    ll1.insert('r');

    int nodeNumber = 5;
    //Node number starts from 1

    ll1.createLoop(nodeNumber);
    bool result = ll1.doesLoopExist();
    if(result == true)
    {
        std::cout <<"Loop exist in the Linked List\n";
    }
    else
    {
        std::cout <<"Loop does not exist in the Linked List\n";
    }

    int len = ll1.lengthOfLoop();
    std::cout << "Length of Loop is " << len <<"\n";

    exit(0);
}

std::move is used to indicate that an object t may be “moved from”, i.e. allowing the efficient transfer of resources from t to another object. It is defined in header <utility>.

Reference: Introduction to Algorithms The Algorithm Design Manual Data Structures and Algorithms Made Easy

Tags: Cpp, Algorithm, Linked-List, Data-Structure