Drawing Book | HackerRank

This is an easy hackerrank challenge which will help you to become good at competitive programming. There are various competitive programming websites like CodeChef, HackerEarth, Codeforces where you can practice coding.

Brie’s Drawing teacher asks her class to open their books to a page number. Brie can either start turning pages from the front of the book or from the back of the book. She always turns pages one at a time. When she opens the book, page 1 is always on the right side:

When she flips page 1, she sees pages 2 and 3. Each page except the last page will always be printed on both sides. The last page may only be printed on the front, given the length of the book. If the book is n pages long, and she wants to turn to page p, what is the minimum number of pages she will turn? She can start at the beginning or the end of the book.

Read full problem here : Drawing Book

Except first (and last page if number of pages in the book is even), a reader always sees two pages where page number on left page is even and page number on right page is odd. So number of flips from the front page to any pages p and p+1 is equal. Thus if p is even then increment p by 1 and calculate number of minimum number of flips to p from front or back of the book.

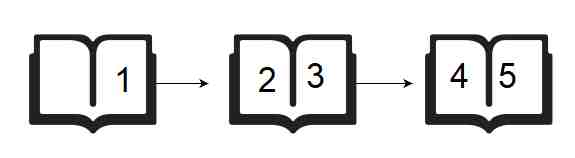
Here for p = 2 and p = 3, number of flips from front page is 1.

if (p % 2 == 0)
{
    p = p + 1;
}

Here p is the page that Brie’s teacher wants her to turn to.

An array right_page_number stores the page number on the right page which is an odd number (p is also an odd number after increment) and an integer variable page_num stores the current page number which is entered in the array.

To enter page numbers on right pages, a for loop is used and it is iterated for n/2 times where n is number of pages in the book. For eg. for n = 5, loop will run for 2 times (i.e. 5/2 = 2 in integer variable).

int page_num = 1;
std::vector<int> right_page_number;
for (int i = 0; i <= n/2; ++i)
{
    right_page_number.push_back(page_num);
    page_num += 2;
}

For the above example the array right_page_number is :

The index of the array right_page_number tells the number of flips from the front page to the page number. For eg. number of flips from front to page number 4 (p = 5) is 2.

The number of flips from the back of the book is n/2 – index of that page number in the array right_page_number. Here n is number of pages in the book. For eg. number of flips from the back to page number 2 (p = 3) is 2 – 1 = 1 (n/2 – 1).

auto index = std::find(right_page_number.begin(), right_page_number.end(), p);

int num_of_flips_from_front = std::distance(right_page_number.begin(), index);
int num_of_flips_from_back = (n/2) – std::distance(right_page_number.begin(), index);

The the minimum number of pages Brie must turn in order to arrive at page p is minimum of num_of_flips_from_front and num_of_flips_from_back.

int min_flips = std::min(num_of_flips_from_front, num_of_flips_from_back);

#include <iostream>
#include <vector>
#include <algorithm>

int flips_count(int n, int p) 
{
    if (p % 2 == 0)
    {
        p = p + 1;
    }

    int page_num = 1;
    std::vector<int> right_page_number;
    for (int i = 0; i <= n/2; ++i)
    {
        right_page_number.push_back(page_num);
        page_num += 2;
    }

    auto index = std::find(right_page_number.begin(), right_page_number.end(), p);

    int num_of_flips_from_front = std::distance(right_page_number.begin(), index);
	int num_of_flips_from_back = (n/2) - std::distance(right_page_number.begin(), index);

    int min_flips = std::min(num_of_flips_from_front, num_of_flips_from_back);

    return min_flips;
}

int main()
{
    int n, p;
    std::cin >> n; //number of pages in the book
    std::cin >> p; //page to open

    int result = flips_count(n, p);
    std::cout << result << "\n";
    return 0;
}

View this code on Github.

If you have a better solution then please comment below the link to the code.