Kruskal's Algorithm | Minimum Spanning Tree
When edges connects all vertices in a graph and form a tree then it is known as spanning tree. While connecting edges no cycle should be formed. A minimum spanning tree is the spanning tree whose sum of edge weights is as small as possible.
Initially no vertices are connected to any other vertex means the spanning tree does not contain any edges, it only contain vertices. Kruskal’s algorithm adds an edge to the tree which has the smallest weight if it does not create a cycle.
Kruskal’s algorithm is a greedy algorithm, because at each step it adds an edge with minimum possible weight.
Here are the given edges and their weight, arranged in increasing order.

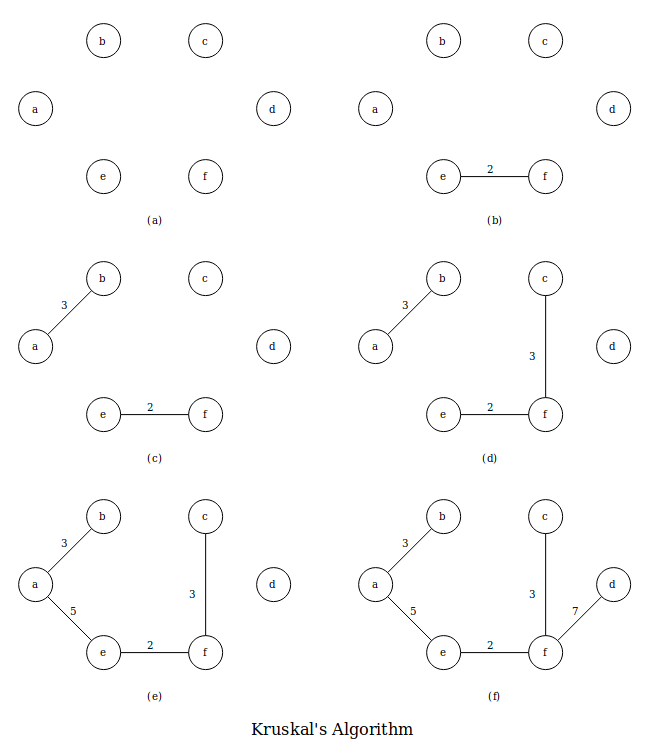
In the above fig. algorithm add edges with minimum weight and if it does not create cycle. Weight of edge b - e is less than edge d – f but it was creating a cycle a – b – e – a , so it was not added.
In fig. (c) there are two disjoint sets. First set contains {a, b} and representative of this set is a whereas second set contains {e, f} and representative of this set is e. Thus a and b forms a tree and e and f forms another tree. All vertices in a tree have same representative (or parent).
std::size_t find_set(std::size_t vertex)
{
auto it = vertices[vertex].parent;
std::size_t parent_id = it->id;
if (it != &vertices[vertex])
{
parent_id = find_set(it->id);
}
return parent_id;
}
find_set tells us about the representative of the vertex. find_set(a) = find_set(b) and find_set(a) ≠ find_set(b).
void make_set(std::size_t vertex)
{
vertices[vertex].parent = &vertices[vertex];
vertices[vertex].rank = 0;
}
make_set is the first function algorithm calls. Initially, number of disjoint sets is equal to the number of vertices, since there is no spanning tree and no vertices are connected like in fig. (a). It sets rank of each vertex to 0 and make them representative of their set since there is only one element in the set, which is the vertex.
void link(std::size_t to, std::size_t from)
{
if (vertices[to].rank > vertices[from].rank)
{
vertices[from].parent = &vertices[to];
}
else
{
vertices[to].parent = &vertices[from];
if (vertices[to].rank == vertices[from].rank)
{
vertices[from].rank = vertices[from].rank + 1;
}
}
}
to is the vertex which is already in a spanning tree and from is the vertex which is being added to the tree.
void union_(std::size_t ver1, std::size_t ver2)
{
link( find_set(vertices[ver1].id), find_set(vertices[ver2].id) );
}
void kruskal()
{
for (std::size_t i = 0; i < vertices.size(); i++)
{
make_set(i);
}
//sort according to weight in increasing order
std::sort(edge_weight.begin(), edge_weight.end(),
[](/Const auto& left, const auto& right)
{ return left.second < right.second; } );
for (auto& e: edge_weight)
{
if ( find_set(vertices[e.first.first].id)
!= find_set(vertices[e.first.second].id) )
{
processed.insert(e.first.first);
processed.insert(e.first.second);
cost = cost + e.second;
union_(e.first.first, e.first.second);
}
}
std::cout << "The total cost is : " << cost << "\n";
}
After function make_set is called, the edges are sorted in increasing order according to their weight. Edges are added only if they are not in the same set means only if they do not have same parent.
In fig. (e) edge-weight of b – e is smaller than that of d - f but since b and e belongs to same set and if it is added a cycle will create in the graph.
#include <iostream>
#include <vector>
#include <map>
#include <unordered_set>
#include <algorithm>
class Graph
{
std::size_t cost = 0;
struct Vertex
{
std::size_t id;
Vertex * parent = nullptr;
std::size_t rank;
Vertex(std::size_t id) : id(id) {}
};
using edges = std::pair<std::size_t, std::size_t>;
std::vector<Vertex> vertices = {};
std::vector< std::pair<edges, std::size_t> > edge_weight;
std::unordered_set<std::size_t> processed = {};
public:
Graph(std::size_t);
void add_edge(std::size_t, std::size_t, int);
void kruskal();
private:
void make_set(std::size_t);
void link(std::size_t, std::size_t);
void union_(std::size_t, std::size_t);
std::size_t find_set(std::size_t);
};
Graph::Graph(std::size_t size)
{
vertices.reserve(size);
for (int i = 0; i < size; i++)
{
vertices.emplace_back(i);
}
}
std::size_t Graph::find_set(std::size_t vertex)
{
auto it = vertices[vertex].parent;
std::size_t parent_id = it->id;
if (it != &vertices[vertex])
{
parent_id = find_set(it->id);
}
return parent_id;
}
void Graph::make_set(std::size_t vertex)
{
vertices[vertex].parent = &vertices[vertex];
vertices[vertex].rank = 0;
}
void Graph::link(std::size_t to, std::size_t from)
{
if (vertices[to].rank > vertices[from].rank)
{
vertices[from].parent = &vertices[to];
}
else
{
vertices[to].parent = &vertices[from];
if (vertices[to].rank == vertices[from].rank)
{
vertices[from].rank = vertices[from].rank + 1;
}
}
}
void Graph::union_(std::size_t ver1, std::size_t ver2)
{
link( find_set(vertices[ver1].id),
find_set(vertices[ver2].id) );
}
void Graph::add_edge(std::size_t src, std::size_t dest, int weight)
{
if (src == dest)
{
throw std::logic_error("src == dest");
}
if (src < 0 || vertices.size() <= src)
{
throw std::out_of_range("src");
}
if (dest < 0 || vertices.size() <= dest)
{
throw std::out_of_range("dest");
}
int flag = 0;
for (auto& it: edge_weight)
{
if (it.first.first == src && it.first.second == dest)
{
flag = 1;
break;
}
}
if (flag == 0)
{
//insert vertices with their associated weight
edge_weight.push_back({ {src, dest}, weight});
}
else
{
throw std::logic_error("existing edge");
}
}
void Graph::kruskal()
{
for (std::size_t i = 0; i < vertices.size(); i++)
{
make_set(i);
}
//sort according to weight in increasing order
std::sort(edge_weight.begin(), edge_weight.end(),
[](/Const auto& left, const auto& right)
{ return left.second < right.second; } );
for (auto& e: edge_weight)
{
if ( find_set(vertices[e.first.first].id)
!= find_set(vertices[e.first.second].id) )
{
processed.insert(e.first.first);
processed.insert(e.first.second);
cost = cost + e.second;
union_(e.first.first, e.first.second);
}
}
std::cout << "The total cost is : " << cost << "\n";
}
int main()
{
Graph grp(9);
grp.add_edge(0, 1, 4);
grp.add_edge(0, 2, 8);
grp.add_edge(1, 2, 11);
grp.add_edge(1, 3, 8);
grp.add_edge(3, 4, 2);
grp.add_edge(4, 2, 7);
grp.add_edge(2, 5, 1);
grp.add_edge(5, 4, 6);
grp.add_edge(3, 6, 7);
grp.add_edge(3, 8, 4);
grp.add_edge(5, 8, 2);
grp.add_edge(6, 7, 9);
grp.add_edge(6, 8, 14);
grp.add_edge(7, 8, 10);
grp.kruskal();
}
Compile with command g++ -std=c++14 kruskal.cpp -o kruskal
View this code on Github.
Reference: Introduction to Algorithms The Algorithm Design Manual Data Structures and Algorithms Made Easy Competitive Programmer’s Handbook - Antti Laaksonen