All data in computer is represented in binary i.e. in 0 or 1. Computers or machines do not understand our languages, they understand bits. Generally programmer do not care about operations at the bit level. But sometimes a programmer has to dive in a deeper level and work on bits.

Bits representation

In programming, an n bit integer is stored as a binary number that consists of n bits. So a 32-bit integer consists of 32 bits and 64 bit integer consists of 64 bits. In C++ programming language int data type is 16-bit, 32-bit and 64-bit type. see here

Here is the bit representation of 32 bit int number 10:
00000000000000000000000000001010

In C++, int is either signed or unsigned and so a bit representation is either signed or unsigned.

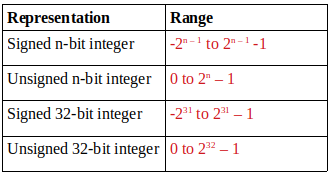
In a signed representation, first bit represents the sign of a number (0 for positive and 1 for negative), and remaining n-1 bits contains the magnitude of the number.

There is a connection between a signed and an unsigned representation. A signed number -x equals an unsigned number 2ⁿ – x.
-x (signed) = 2ⁿ - x (unsigned)

1
2
3
4
int a = -10;
unsigned int b = a;
std::cout << a << "\n"; /* -10 */
std::cout << b << "\n"; /* 4294967286 */

In a signed representation, the next number after 2^{n – 1} – 1 is -2ⁿ – 1, and in an unsigned representation, the next number after 2ⁿ – 1 is 0.

Bit Operations

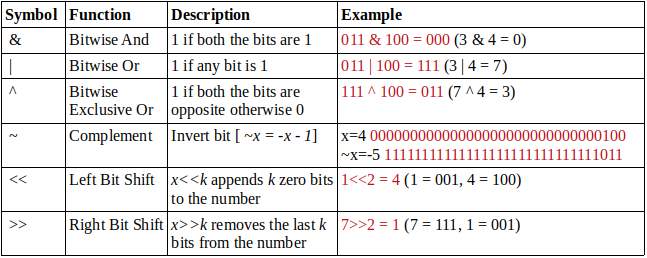
We can use & operator to check if a number is even or odd. If x & 1 = 0 then x is even and if x & 1 = 1 then x is odd. We can also say that, x is divisible by 2^k exactly when x & (2^k – 1) = 0.

x<<k corresponds to multiplying x by 2^k, and x>>k corresponds to dividing x by 2^k rounded down to an integer.

Common Bit Tasks

Binary representation of unsigned int:

1
2
3
4
5
6
7
8
9
10
void binary(unsigned int num)
{
	for(int i = 256; i > 0; i = i/2) {
		if(num & i) 
			std::cout << "1 ";
		else
			std::cout << "0 ";
	}
	std::cout << std::endl;
}

Setting Bit at position:

1
2
3
4
5
int set_bit(int num, int position)
{
	int mask = 1 << position;
	return num | mask;
}

Getting Bit at position:

1
2
3
4
5
bool get_bit(int num, int position)
{
	bool bit = num & (1 << position);
	return bit;
}

Clearing Bit at position:

1
2
3
4
5
int clear_bit(int num, int position)
{
	int mask = 1 << position;
	return num & ~mask;
}

Representing Sets

Bits representation of an integer are 0-indexed and the index starts from right side i.e. least significant bit. So we can represent every subset of the set {0, 1, 2, ..., n-1} as an n bit integer and whose bits indicate which element belongs to the subset. If bit at index 3 is 1 and at index 4 is 0 in binary representation of a number, then 3 belongs to the subset and 4 does not belong to the subset.

For a 32-bit integer, the set is {0, 1, 2,…, 31} and the subset is {1, 3, 4, 8}. The binary representation of the set is: 00000000000000000000000100011010
and decimal representation is 2⁸ + 2⁴ + 2³ + 2¹ = 282.

Code to form subset and add elements to it:

1
2
3
4
5
6
7
8
9
int add_elements_to_subset()
{
	int subset = 0;
	subset = subset | (1 << 1);
	subset = subset | (1 << 3);
	subset = subset | (1 << 4);
	subset = subset | (1 << 8);
	return subset;
}

Code to print elements of the subset:

1
2
3
4
5
6
7
void printing_subset(int subset)
{
	for (int i = 0; i < 32; i++) 
	{
		if (subset & (1 << i)) std::cout << i << " ";
	}
}

Additional functions

The g++ compiler provides the following functions for counting bits:
• __builtin_clz(x): the number of zeros at the beginning of the number
• __builtin_ctz(x): the number of zeros at the end of the number
• __builtin_popcount(x): the number of ones in the number
• __builtin_parity(x): the parity (even or odd) of the number of ones

Get this post in pdf format

Reference:
Competitive Programmer’s Handbook - Antti Laaksonen