Circular Array Rotation | HackerRank
This is an easy hackerrank challenge which will help you to become good at competitive programming. There are various competitive programming websites like CodeChef, HackerEarth, Codeforces where you can practice coding.
Problem :
John Watson knows of an operation called a right circular rotation on an array of integers. One rotation operation moves the last array element to the first position and shifts all remaining elements right one. To test Sherlock’s abilities, Watson provides Sherlock with an array of integers. Sherlock is to perform the rotation operation a number of times then determine the value of the element at a given position. For each array, perform a number of right circular rotations and return the value of the element at a given index.
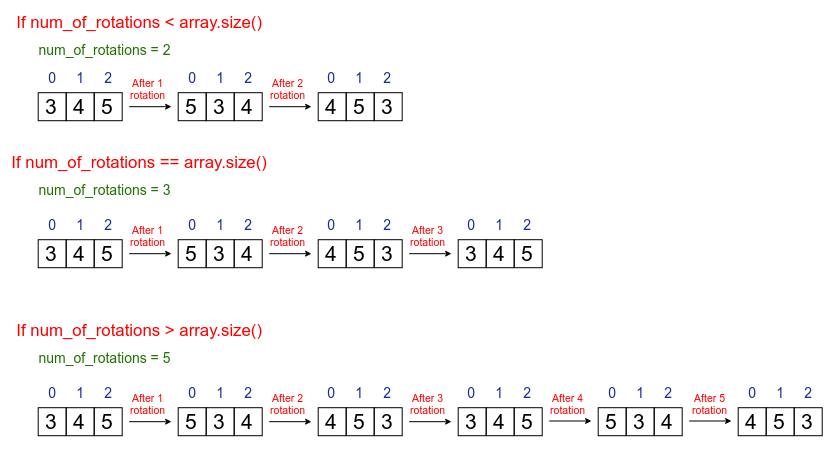
For example, array a = [3, 4, 5], number of rotations, k = 2 and indices to check, m = [1, 2].
First we perform the two rotations:
[3, 4, 5] → [5, 3, 4] → [4, 5, 3]
Now return the values from the zero-based indices 1 and 2 as indicated in the m array.
a[1] = 5
a[2] = 3
Read full problem here : Circular Array Rotation
Solution :
array is the input array, integer variable num_of_rotations stores the number of rotations to be performed on the input array and array indices_to_check stores the indices to be checked after rotation.
If number of rotations is equal to the size of the input array then input array and array after rotation are same.
If number of rotations is greater than the size of the input array then array after num_of_rotations times rotation is equal to the array after num_of_rotations – array.size() times rotations.
For eg. if the size of array is 3 and number of rotations are 5 then array after 5 rotations is equal to the array after 2 rotations.
1
2
3
4
5
int arr_size = array.size();
while (num_of_rotations > arr_size)
{
num_of_rotations = num_of_rotations - arr_size;
}
If we imagine array as a circular array then element after the last element is the element at the first position. So after first circular rotation the last element is moved to the first position and the element at first position is moved to second position and so on all the elements are moved to maintain the order of the array.
For eg. in the array [3, 4, 5] after first rotation 5 is moved to the first position and the element after 5 in circular array is 3 so 3 comes after 5 and so on . After first rotation the array is [5, 3, 4].
Instead of rotating step by step, we declare an array new_array which stores the elements in order after num_of_rotations times rotation. The first element after all rotations on the input array is array[array.size() - num_of_rotations].
For eg. in the array = [1, 2, 3, 4, 5, 6] and num_of_rotations is 3, the new_array will store elements from index array.size() - num_of_rotations to last index in the array i.e. elements 4, 5, 6.
new_array = [4, 5, 6]
And then the elements from index 0 to index array.size() - num_of_rotations – 1 are added to the new_array i.e. elements 1, 2, 3.
new_array = [4, 5, 6, 1, 2, 3].
1
2
3
4
5
6
7
8
9
std::vector<int> new_array;
for (int i = arr_size - num_of_rotations; i < arr_size; ++i)
{
new_array.push_back(array[i]);
}
for (int i = 0; i < arr_size - num_of_rotations; ++i)
{
new_array.push_back(array[i]);
}
To store the elements at the indices stored in the array indices_to_check, an array res is declared.
1
2
3
4
5
6
7
std::vector<int> res;
for(int i = 0; i < indices_to_check.size(); ++i)
{
int idx = indices_to_check[i];
int val = new_array[idx];
res.push_back(val);
}
C++ Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
std::vector<int> circular_array_rotation(const std::vector<int>& array, int num_of_rotations, const std::vector<int>& indices_to_check)
{
int arr_size = array.size();
while (num_of_rotations > arr_size)
{
num_of_rotations = num_of_rotations - arr_size;
}
std::vector<int> new_array;
for (int i = arr_size - num_of_rotations; i < arr_size; ++i)
{
new_array.push_back(array[i]);
}
for (int i = 0; i < arr_size - num_of_rotations; ++i)
{
new_array.push_back(array[i]);
}
std::vector<int> res;
for(int i = 0; i < indices_to_check.size(); ++i)
{
int idx = indices_to_check[i];
int val = new_array[idx];
res.push_back(val);
}
return res;
}
int main()
{
int num_of_elements, num_of_rotations, num_of_indices_to_check;
std::cin >> num_of_elements >> num_of_rotations >> num_of_indices_to_check;
std::vector<int> array(num_of_elements);
std::vector<int> indices_to_check(num_of_indices_to_check);
for (int i = 0; i < num_of_elements; ++i)
{
std::cin >> array[i];
}
for (int i = 0; i < num_of_indices_to_check; ++i)
{
std::cin >> indices_to_check[i];
}
std::vector<int> result = circular_array_rotation(array, num_of_rotations, indices_to_check);
for (int i = 0; i < result.size(); ++i)
{
std::cout << result[i] << "\n";
}
}
View this code on Github.
Better solutions exist for the problem, but I tried to explain in the simplest way. If you have a better solution then please share the link to the code in the comments below.
Other Competitive Programming Problems and Solutions
Drawing Book HackerRank Challenge
Migratory Birds - HackerRank Challenge