Bank Robbers - CodinGame | C++ Implementation
The problem is from CodinGame with difficulty level Easy and tagged under Loops and Mathematics.
Problem:
A gang of R foolish robbers decides to heist a bank. In the bank there are V vaults (indexed from 0 to V-1). The robbers have managed to extract some information from the bank’s director:
- The combination of a vault is composed of
Ccharacters (digits/vowels). - The first
Ncharacters consist of digits from 0 to 9. - The remaining characters consist of vowels (A, E, I, O, U).
CandNmay be the same or different for different vaults.
All the robbers work at the same time. A robber can work on one vault at a time, and a vault can be worked on by only one robber. Robbers deal with the different vaults in increasing order.
A robber tries the combinations at the speed of combination per second. He tries all the possible combinations, i.e. he continues to try the untried combinations even after he has found the correct combination. Once he finishes one vault, he moves on to the next available vault, that is the vault with the smallest index among all the vaults that have not been worked on yet. The heist is finished when the robbers have worked on all the vaults.
Assume it takes no time to move from one vault to another.
You have to output the total time the heist takes.
Read full problem here : Bank Robbers
Solution:
The good things is that the robber will continue to try untried combinations ever after he has found the correct combination. So we have to find the total number of combinations for each vault.
For each vault, first N characters are digits from 0 to 9 and remaining C-N characters are vowels.
For eg. C = 5 and N = 2 i.e. _ _ _ _ _
To fill first slot there are 10 ways, to fill second ways there are 10 and to fill third slot there are 10 ways. To fill fourth slot there are 5 ways and to fill fifth slot there are 5 ways. Thus total number of combinations = 10 * 10 * 10 * 5 * 5 = 103 * 52
The formula to find the number of combinations for a vault is 10^N * 5^(C-N).
While we enter C and N for each vault, we calculate the number of combinations for each vault and store them in an array vault_time.
1
2
3
4
5
6
7
8
9
std::vector<int> vault_time(V, 0);
for (int i = 0; i < V; ++i)
{
int C;
int N;
std::cin >> C >> N; std::cin.ignore();
vault_time[i] += pow(10, N) * pow(5, C-N);
}
To make sense, number of robbers should be equal to or less than the number of vaults. We will make an array robber_time, which will store the time take by each robber to open vaults.
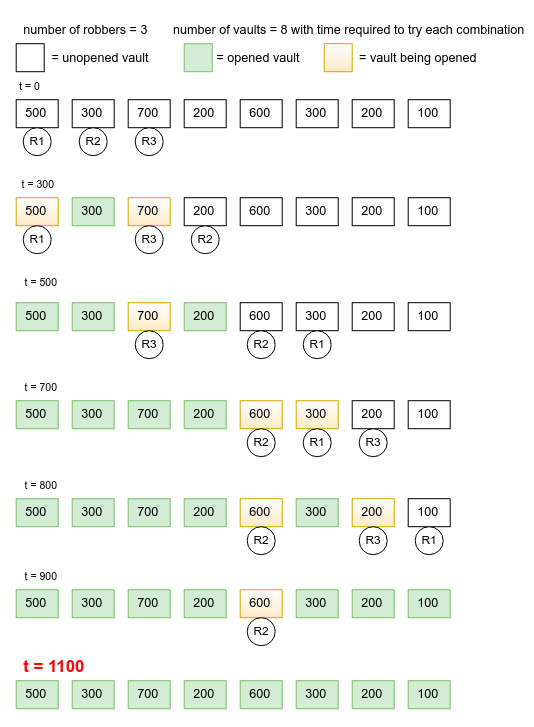
In the above fig. it is time taken by each vault.
It is given than robbers deal with each vault in increasing order of index number. Initially all robbers are idle. So all robbers choose each vault in the increasing order of index number. For eg. if there are 3 robbers and 8 vaults then robbers choose first 3 vaults.
1
2
3
4
5
6
7
8
std::vector<int> robber_time(num_of_robbers, 0);
int vaults_opened = 0;
for (int i = 0; i < num_of_robbers; ++i)
{
robber_time[i] += vault_time[vaults_opened];
vaults_opened++;
}
Now, robber_time stores the time each robber has spent. To proceed further, we will choose the robber who has spent less time. Robber who has spent less time means he has recently opened a vault and currently he is idle while other robbers are busy. For eg. in the above fig. at time = 300 R1 is idle while others are busy.
So now everytime we will choose a robber with smallest spent time and assign him to the next vault until all vaults are opened.
1
2
3
4
5
6
7
while (vaults_opened < vault_time.size())
{
std::sort(robber_time.begin(), robber_time.end());
robber_time[0] += vault_time[vaults_opened];
vaults_opened++;
}
To find the total time spent we have to find the robber who was last to open the vault means whose sum of total time spent to largest compared to other robbers.
1
auto total_time = std::max_element(robber_time.begin(), robber_time.end());
Here total_time is an iterator.
C++ Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
int calculate_heist_time(std::vector<int>& vault_time, int num_of_robbers)
{
std::vector<int> robber_time(num_of_robbers, 0);
int vaults_opened = 0;
for (int i = 0; i < num_of_robbers; ++i)
{
robber_time[i] += vault_time[vaults_opened];
vaults_opened++;
}
while (vaults_opened < vault_time.size())
{
std::sort(robber_time.begin(), robber_time.end());
robber_time[0] += vault_time[vaults_opened];
vaults_opened++;
}
auto total_time = std::max_element(robber_time.begin(), robber_time.end());
return *total_time;
}
int main()
{
int R;
std::cin >> R; std::cin.ignore();
int V;
std::cin >> V; std::cin.ignore();
std::vector<int> vault_time(V, 0);
for (int i = 0; i < V; ++i)
{
int C;
int N;
std::cin >> C >> N; std::cin.ignore();
vault_time[i] += pow(10, N) * pow(5, C-N);
}
std::cout << calculate_heist_time(vault_time, R) << "\n";
}
View this on Github
If you have another solution then please share it in the comments below.
Other Competitive Programming Problems and Solutions