Stock Exchange Losses - CodinGame | C++ Implementation
Table of Content
- Problem: - {:.} Input - {:.} Output
- Solution: - {:.} C++ Implementation - {:.} Other Competitive Programming Problems and Solutions
The problem is from CodinGame with difficulty level Medium.
Problem:
A finance company is carrying out a study on the worst stock investments and would like to acquire a program to do so. The program must be able to analyze a chronological series of stock values in order to show the largest loss that it is possible to make by buying a share at a given time t0 and by selling it at a later date t1. The loss will be expressed as the difference in value between t0 and t1. If there is no loss, the loss will be worth 0.
Input
Line 1: the number n of stock values available.
Line 2: the stock values arranged in order, from the date of their introduction on the stock market V1 until the last known value Vn. The values are integers.
Output
The maximal loss p, expressed negatively if there is a loss, otherwise 0.
Read full problem here : Stock Exchange Losses
Solution:
The input values are the stock prices at various times. We store these stock prices in an integer vector called values. The index of the vector represents the time and the element at that index is the stock price at that time.
The three given test cases are:
1
2
3
4
5
6
Input
6
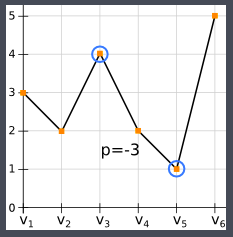
3 2 4 2 1 5
Output
-3
1
2
3
4
5
6
Input
6
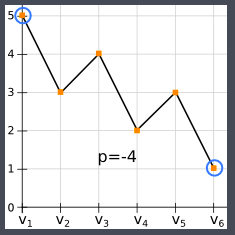
5 3 4 2 3 1
Output
-4
1
2
3
4
5
6
Input
5
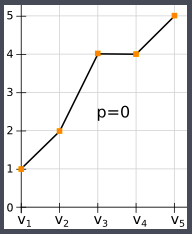
1 2 4 4 5
Output
0
From the test cases, we can see that there is a loss only when the stock price at time t2 is less than the stock price at time t1 (where t2 > t1). Otherwise, the loss is 0.
Therefore, we only need to process further when values[i] > values[j], where i and j are iterable variables in a loop. We initialize i to 0 and j to i+1.
Before we proceed, we should initialize all the variables that we need.
1
2
3
4
int loss = std::numeric_limits<int>::max();
int maxima = std::numeric_limits<int>::min();
int minima = std::numeric_limits<int>::max();
int maxima_index = 0, minima_index = 0;
While i = 0, j will iterate from i+1 to values.size() - 1.
And, when condition values[i] > values[j] is false, then the value of i becomes the last value of j.
In fig 1, i = 0 and at j = 2 (i.e V3), the condition values[i] > values[j] is false. So the new value of i is 2 and value of j is 3 (i.e i+1).
In fig 1, from V1 to V2, the condition values[i] > values[j] is true. So this is one section of graph where we will calculate loss. This loss will be stored in an integer variable local_loss. There will be many sections in graph where we will calculate the local_loss and update variable loss with lowest values (i.e. highest loss). The values will be in negative so lowest value means highest loss.
Similarly, integer variable maxima and minima will store the maximum and minimum values in the graph, but the condition is that maxima_index < minima_index.
As the program proceeds, the value of these variables change.
The value of variables maxima and minima will change only when values[i] >= maxima. This means we have found the new maximum in the graph, so maxima is updated. And minima is updated because its index must be greater than the index of maxima.
So, we can only update value of minima, maxima, minima_index and maxima_index if conditions values[i] > values[j] and local_loss < loss and values[i] >= maxima are true.
In fig 1, from V1(i = 0) to V2(j = 1), maxima is 3 and minima is 2 and loss is -1. From V3(i = 2) to V4(j = 3), the loss becomes -2.The values[i](=4) is also greater than maxima(=3). Thus all conditons values[i] > values[j] and local_loss < loss and values[i] >= maxima are true. So maxima and minima is updated.
At V3(i = 2) and V5(j = 4) again all conditions are true and new value of loss is calculated.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int i = 0;
int j = i+1;
while (j < values.size())
{
if (values[i] > values[j])
{
int local_loss = values[j] - values[i];
if (local_loss < loss)
{
loss = local_loss;
if (values[i] >= maxima)
{
maxima = values[i];
maxima_index = i;
minima = values[j];
minima_index = j;
}
}
}
else if (values[i] < values[j])
{
i = j;
j = i;
}
j++;
}
For the third test case, the condition values[i] > values[j] is never true. As a result, the loss variable is never updated and retains its initial value, which is the highest value an integer can store.
Since minima and maxima are also never updated, their indices remain 0. Therefore, the loss will be 0 when we calculate it using the formula loss = values[minima_index] - values[maxima_index].
C++ Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <vector>
#include <limits>
int largest_loss(std::vector<int>& values)
{
int loss = std::numeric_limits<int>::max();
int maxima = std::numeric_limits<int>::min();
int minima = std::numeric_limits<int>::max();
int maxima_index = 0, minima_index = 0;
int i = 0;
int j = i+1;
while (j < values.size())
{
if (values[i] > values[j])
{
int local_loss = values[j] - values[i];
if (local_loss < loss)
{
loss = local_loss;
if (values[i] >= maxima)
{
maxima = values[i];
maxima_index = i;
minima = values[j];
minima_index = j;
}
}
}
else if (values[i] < values[j])
{
i = j;
j = i;
}
j++;
}
loss = values[minima_index] - values[maxima_index];
return loss;
}
int main()
{
int n;
std::cin >> n; std::cin.ignore();
std::vector<int> values(n);
for (int i = 0; i < n; i++) {
std::cin >> values[i];
std::cin.ignore();
}
int loss = largest_loss(values);
std::cout << loss << std::endl;
}
Check out this on Github
If you have a different solution for Stock Exchange Losses, please share it in the comments below.
Other Competitive Programming Problems and Solutions