Breadth First Search using Adjacency List | Graph traversal

Publish date: 2018-03-06
Tags: Cpp, Algorithm, Graph-Algorithms

Breadth first search (BFS) explores the graph level by level. First it explore every vertex that is connected to source vertex. If the vertex is discovered, it becomes gray or black. Initially all the vertices are white.

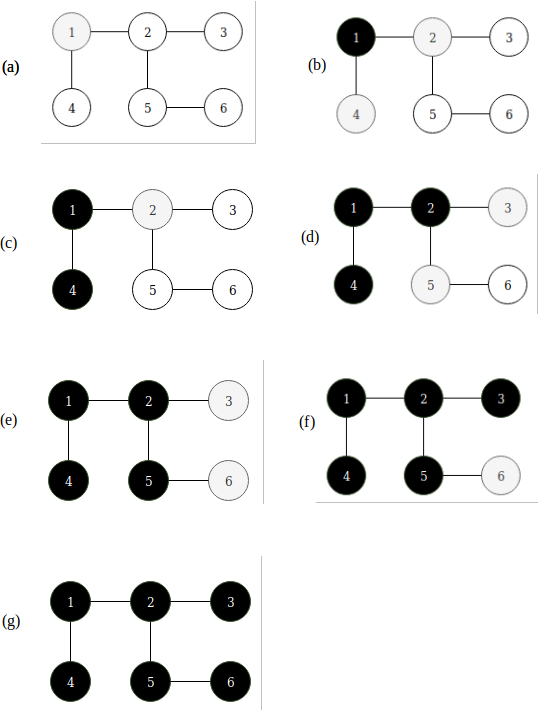
Breadth First Search

If vertex 1 is the source vertex, then it is at level 0. Vertex 2 and 4 are at level 1 and vertex 3 and 5 are at level 2. Vertex 6 is at level 3. Thus, we can calculate the distance from source vertex to other vertex.

When vertex 1 is discovered it becomes gray and when it is reached it become black. When vertex 1 is reached vertex 2 and 4 are discovered and they become gray and so on. So the vertices are white, then they become gray and then black.

To store distance from the source vertex and to know if the vertex is discovered, we need a data structure to store value for the given vertex.

Here is the implementation of the function breadthFirstSearch.

enum Color {WHITE, GRAY, BLACK};
enum { INFINITY = std::numeric_limits<int>::max() };
  struct Vertex
  {
     int id;
     int distance;
     Color color;

     Vertex(int _id) : id(_id),
                       color(Color::WHITE),
                       distance(INFINITY)
                       {}
  };

void breadthFirstSearch(int s)
{
   vertices[s].color = GRAY;
   vertices[s].distance = 0;
   std::queue<Vertex> q;
   q.push(vertices[s]);
   while (!q.empty())
   {
      auto u = q.front();
      q.pop();
      for (const auto& v : adjList[u.id])
      {
         if (vertices[v].color == WHITE)
         {
            vertices[v].color = GRAY;
            vertices[v].distance = u.distance + 1;
            q.push(vertices[v]);
         }
      }
      u.color = BLACK;
   }
}

Variable color in the struct Vertex stores color of the given vertex and variable distance stores distance of the vertex from the source vertex. In the function the source vertex is passed.

The time complexity of Breadth First Search is O(n+m) where n is the number of vertices and m is the number of edges.

Here is C++ implementation of Breadth First Search using Adjacency List

#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <limits>

class Graph
{
  int vertex_count;
  enum Color {WHITE, GRAY, BLACK};

  enum { INFINITY = std::numeric_limits<int>::max() };

  struct Vertex
  {
     int id;
     int distance;
     Color color;

     Vertex(int _id) : id(_id),
                       color(Color::WHITE),
                       distance(INFINITY)
                       {}
  };

public:

  std::vector<Vertex> vertices;
  std::vector< std::list<int> > adjList;

  Graph(int);
  void addEdge(int, int);
  void breadthFirstSearch(int);
};

Graph::Graph(int v)
{
   vertex_count = v;
   adjList.resize(vertex_count);
   for (int i = 0; i < vertex_count; i++)
   {
       vertices.push_back( Vertex(i) );
   }
}

void Graph::addEdge(int src, int dest)
{
  //undirected graph
   adjList[src].push_back(dest);
   adjList[dest].push_back(src);
}

void Graph::breadthFirstSearch(int s)
{
   vertices[s].color = GRAY;
   vertices[s].distance = 0;
   std::queue<Vertex> q;
   q.push(vertices[s]);
   while (!q.empty())
   {
      auto u = q.front();
      q.pop();
      for (const auto& v : adjList[u.id])
      {
         if (vertices[v].color == WHITE)
         {
            vertices[v].color = GRAY;
            vertices[v].distance = u.distance + 1;
            q.push(vertices[v]);
         }
      }
      u.color = BLACK;
      std::cout << vertices[u.id].id << " at level " << vertices[u.id].distance <<'\n';
   }
}

int main()
{
   Graph grp(5);
   grp.addEdge(0, 1);
   grp.addEdge(0, 4);
   grp.addEdge(1, 3);
   grp.addEdge(1, 4);
   grp.addEdge(1, 2);
   grp.addEdge(2, 3);
   grp.addEdge(3, 4);
   grp.breadthFirstSearch(2);
}

Output

Output

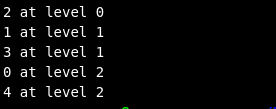
Reference: Introduction to Algorithms The Algorithm Design Manual Data Structures and Algorithms Made Easy Competitive Programmer’s Handbook - Antti Laaksonen

C++: Dijkstra’s Algorithm using STL C++: Bellman Ford Algorithm using STL C++: Depth First Search using Adjacency List

Tags: Cpp, Algorithm, Graph-Algorithms