Heapsort | C++ Implementation
Heapsort is implemented using heap data structure. Heap helps us to represent binary tree without using any pointers. Using heap an array can be viewed as a binary tree and each node of the tree stores an element of the array.
There are two kinds of binary heaps: max-heaps and min-heaps. In max-heap, the value stored at the parent node is greater than the value stored at its children nodes. Thus in a max-heap, root node contains the largest element. In min-heap, the value stored at the parent node is smaller than the value stored at its children nodes. Thus in a min-heap, root node contains the smallest element.
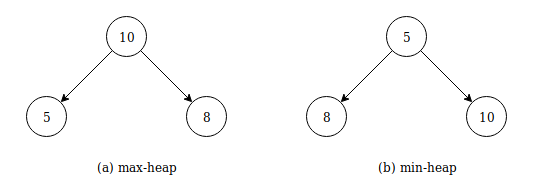
Max-heap is used in heapsort algorithm and min-heap is used in priority queues.
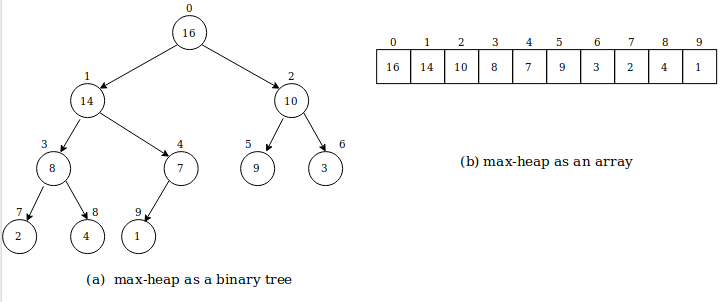
When arr[i] = parent, then left_child = 2*i + 1 and right_child = 2*i + 2.
max_heapify maintains the max-heap property of the heap. The input array, index of the element and size of the array is passed as an argument.
void max_heapify(std::vector<int>& arr, int i, int size_)
{
int largest, l = (2*i) + 1, r = l + 1;
if(l < size_ && arr[l] > arr[i])
largest = l;
else
largest = i;
if(r < size_ && arr[r] > arr[largest])
largest = r;
if(largest != i)
{
std::swap(arr[i], arr[largest]);
max_heapify(arr, largest, size_);
}
}
If arr[i] is largest, then subtree rooted at node i is a max-heap and function terminates. Otherwise, largest stores the index of child whose value is greatest of the three elements and arr[i] is swapped with arr[largest] and thus max-heap property is satisfied at node i. Then max_heapify with node indexed by largest is called to satisfy max-heap property at node largest.
build_max_heap produces a max-heap from an input array.
void build_max_heap(std::vector<int>& arr)
{
for(int i = (arr.size() / 2); i >= 0; i--)
max_heapify(arr, i, arr.size());
}
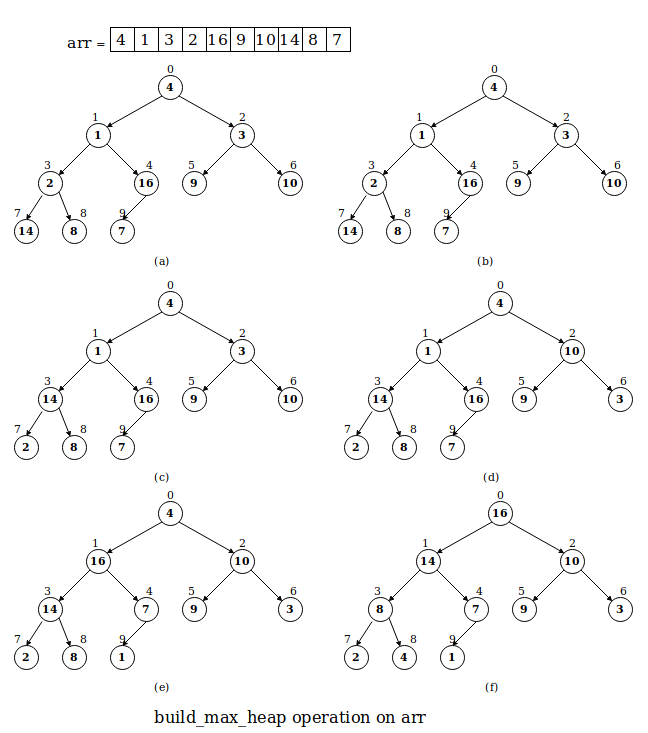
heapsort sorts an array in-place.
void heap_sort(std::vector<int>& arr)
{
build_max_heap(arr);
int sz = arr.size();
for(int i = arr.size() - 1; i > 0; i--)
{
std::swap(arr[0], arr[i]);
sz--;
max_heapify(arr, 0, sz);
}
}
heapsort starts with build_max_heap and now largest element of the array is at index 0. So the first value is swapped with the last value and then the node with largest value is removed from the tree and new max-heap is created with max_heapify.
#include <iostream>
#include <vector>
#include <algorithm>
void max_heapify(std::vector<int>& arr, int i, int size_)
{
int largest, l = (2*i) + 1, r = l + 1;
if(l < size_ && arr[l] > arr[i])
largest = l;
else
largest = i;
if(r < size_ && arr[r] > arr[largest])
largest = r;
if(largest != i)
{
std::swap(arr[i], arr[largest]);
max_heapify(arr, largest, size_);
}
}
void build_max_heap(std::vector<int>& arr)
{
for(int i = (arr.size() / 2); i >= 0; i--)
max_heapify(arr, i, arr.size());
}
void heap_sort(std::vector<int>& arr)
{
build_max_heap(arr);
int sz = arr.size();
for(int i = arr.size() - 1; i > 0; i--)
{
std::swap(arr[0], arr[i]);
sz--;
max_heapify(arr, 0, sz);
}
}
int main()
{
std::vector<int> arr = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
heap_sort(arr);
for(int i = 0; i < arr.size(); i++)
{
std::cout << arr[i] << " ";
}
std::cout << "\n";
return 0;
}
Reference: Introduction to Algorithms The Algorithm Design Manual Data Structures and Algorithms Made Easy Competitive Programmer’s Handbook - Antti Laaksonen
Selection sort Merge Sort Insertion Sort Quicksort