orDer oF succeSsion - CodinGame | C++ Implementation
Table of Content
The problem is from CodinGame with difficulty level Medium.
Problem:
You have to output the order of succession to the British throne of a list of given people. The order is simple: From a descendant A, the next in the order is A’s first child B. Then, the next one is B’s first child C if any and so on. If C has no child, then the next one is B’s second child D. Then D’s children if any. Then B’s third child E… then A’s second child F…
Let’s draw it with a tree:
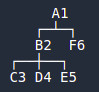
You see the order of succession: begin on the left of the tree, walk to the next level whenever possible otherwise continue to the right. Repeat until the whole tree is covered. Thus, the order is A-B-C-D-E-F.
In fact, in siblings of the same person, the male descendants are ordered before the female descendants. For example, if the order of birth of the children (M for male, F for female) is Fa Ma Me Fe then the order of succession in these siblings is Ma Me Fa Fe.
Ordering rules (a) in order of generation (b) in order of gender (c) in order of age (year of birth)
Outputting rules (a) exclude dead people (but include siblings of dead people) (b) exclude people who are catholic (but include siblings of catholic people)
Constraints
Exactly one people does not have a parent (the parent’s name is replaced by the hyphen -).
Read full problem here : orDer oF succeSsion
Solution:
For each individual, we can store their personal information such as name, parent’s name, year of birth and death, etc. in a struct called Details.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct Details
{
std::string name;
std::string parent_name;
int birth; // year of birth
std::string death;
std::string religion;
std::string gender;
int index;
bool has_child = false;
bool processed = false;
Details * parent;
Details * sibling;
Details * first_child;
Details(){}
Details(std::string name_, std::string parent_name_, int birth_, std::string death_, std::string religion_, std::string gender_, int index_):
name(name_), parent_name(parent_name_), birth(birth_), death(death_), religion(religion_),
gender(gender_), index(index_), parent(nullptr), sibling(nullptr), first_child(nullptr) {}
};
In the main function, we can store the personal information of multiple individuals in a vector of structures called Details. This can be done using the following code:
1
std::vector<Details> family_details;
This creates a new vector called family_details that is capable of storing Details structures.
To determine the first ruler in a given family, we can find the person whose parent does not exist in the family_details vector. This person is considered the first ruler, and we can store their index in the vector in an integer variable called first_ruler_index.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int first_ruler_idx;
for (int i = 0; i < n; i++)
{
std::string name;
std::string parent;
int birth;
std::string death;
std::string religion;
std::string gender;
std::cin >> name >> parent >> birth >> death >> religion >> gender; std::cin.ignore();
if (parent == "-")
{
first_ruler_idx = i;
}
family_details.push_back( Details(name, parent, birth, death, religion, gender, i));
}
If the parent_name field is -, it indicates that the person is the first ruler and their index is stored in first_ruler_index.
Function order_of_succession:
In this function, we pass a vector of Details and an integer variable first_ruler_idx as parameters. The function returns a vector of strings in the order of succession.
We declare a vector of strings rulers and an integer variable curr_ruler_idx. Then, we call the map_parent_children function, which maps the ruler at curr_ruler_idx with his or her children.
To order the rulers, we use a while loop whose condition is always true. In the loop, we check that the person is eligible to rule by making sure they are not dead and their religion is not Catholic. We also set a boolean variable processed for each person to true once they have been processed to ensure that the same person is not processed twice.
1
2
3
4
5
6
7
8
9
10
11
12
13
while (true)
{
if (family[curr_ruler_idx].death == "-" &&
family[curr_ruler_idx].religion != "Catholic" && !family[curr_ruler_idx].processed)
{
rulers.push_back(family[curr_ruler_idx].name);
}
family[curr_ruler_idx].processed = true;
...
...
...
}
After adding the ruler at curr_ruler_idx to the vector ruler, we check if they have a child. If they do, we update the value of curr_ruler_idx to the index of the first child.
Note that the siblings are already ordered according to their age and gender in the map_parent_children function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
while (true)
{
...
if (family[curr_ruler_idx].has_child)
{
curr_ruler_idx = family[curr_ruler_idx].first_child->index;
}
else
{
...
}
map_parent_children(family, curr_ruler_idx);
}
If the current ruler does not have a child, we check if they have a sibling. If they do, we update the value of curr_ruler_idx to the index of the next sibling.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
while (true)
{
...
if (family[curr_ruler_idx].has_child)
{
...
}
else
{
if (family[curr_ruler_idx].sibling != nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].sibling->index;
}
else
{
...
}
}
map_parent_children(family, curr_ruler_idx);
}
If the current ruler does not have a sibling, the next ruler will be the sibling of their parent. If the parent does not have a sibling, we move on to check for the grandparent and so on, until we find the next ruler in the line of succession.
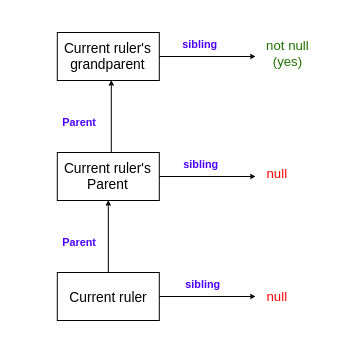
Before processing, we make sure that the current ruler is not equal to the first ruler. If they are equal, it means we have processed everyone in the family and we can terminate the while loop.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
while (true)
{
...
if (family[curr_ruler_idx].has_child)
{
...
}
else
{
if (family[curr_ruler_idx].sibling != nullptr)
{
...
}
else
{
while (curr_ruler_idx != first_ruler_idx &&
family[curr_ruler_idx].parent->sibling == nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].parent->index;
}
if (curr_ruler_idx == first_ruler_idx)
{
break;
}
if (family[curr_ruler_idx].parent->sibling != nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].parent->sibling->index;
}
}
}
map_parent_children(family, curr_ruler_idx);
}
Inside the while loop, we call the map_parent_children function again because the value of curr_ruler_idx may have changed. This ensures that the updated value of curr_ruler_idx is used when mapping the current ruler with their children.
Function map_parent_children :
In this function, we pass a vector of Details called family and an integer variable curr_ruler_idx as parameters. The function maps the ruler at curr_ruler_idx with their children.
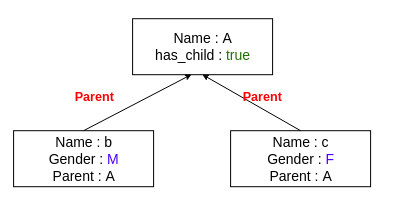
First, we declare two vectors of integers: next_gen_m_idx will store the indices of male children of the ruler at curr_ruler_idx, and next_gen_f_idx will store the indices of female children. These vectors will be used to store the indices of the children in the family vector.
1
2
std::vector<int> next_gen_m_idx; // stores index of male members of next generation
std::vector<int> next_gen_f_idx; // stores index of female members of next generation
We iterate through the family vector and check if the name of the parent of the person at the current index is equal to the name of the ruler at curr_ruler_idx. If it is, the current ruler is the parent of the person we are processing. We then store the index of the current person in either the next_gen_m_idx vector or the next_gen_f_idx vector, depending on their gender.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for (int i = 0; i < family.size(); ++i)
{
if (family[i].parent_name == family[curr_ruler_idx].name)
{
family[curr_ruler_idx].has_child = true;
family[i].parent = &family[curr_ruler_idx]; // mapping parent
if (family[i].gender == "M")
{
next_gen_m_idx.push_back(i);
}
else
{
next_gen_f_idx.push_back(i);
}
}
}
In the case of siblings, the eldest sibling is the next ruler. So, we sort both the next_gen_m_idx and next_gen_f_idx vectors according to the age of the siblings. Then, we call the map_siblings function to determine the order of succession among the siblings.
1
2
3
4
5
6
7
8
9
10
11
12
13
//sort both vectors according to age
if (family[curr_ruler_idx].has_child)
{
static const auto by_age = [family](const int i, const int j)
{
return family[i].birth < family[j].birth; // year of birth is smaller means age is bigger
};
std::sort(next_gen_m_idx.begin(), next_gen_m_idx.begin(), by_age);
std::sort(next_gen_f_idx.begin(), next_gen_f_idx.begin(), by_age);
map_siblings(next_gen_m_idx, next_gen_f_idx, family, curr_ruler_idx);
}
Function map_siblings :
In this function, we pass two integer vectors called male_idx and female_idx, a vector of Details called family, and an integer variable curr_ruler_idx as parameters. The male_idx and female_idx vectors are already sorted according to the ages of the siblings. The function’s purpose is to form links between the siblings to determine the order of succession.
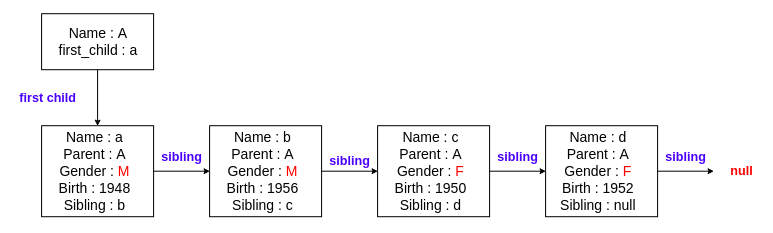
We first check if the male_idx vector is empty. If it is not, we set the first_child of the current ruler to the child at index 0 of the male_idx vector.
If the size of male_idx is 1 and the female_idx vector is not empty, we set the sibling of the child at index 0 of male_idx to the child at index 0 of female_idx.
Otherwise, we iterate through the male_idx vector and link the siblings.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
if (!male_idx.empty())
{
family[curr_ruler_idx].first_child = &family[male_idx[0]];
if (male_idx.size() == 1)
{
if (!female_idx.empty())
{
family[male_idx[0]].sibling = &family[female_idx[0]];
}
}
else
{
for (int i = 0; i < male_idx.size()-1; ++i)
{
family[male_idx[i]].sibling = &family[male_idx[i+1]];
}
}
}
else
{
...
}
If the male_idx vector is empty, the first_child of the current ruler is the child at index 0 of the female_idx vector.
1
2
3
4
5
6
7
8
if (!male_idx.empty())
{
...
}
else
{
family[curr_ruler_idx].first_child = &family[female_idx[0]];
}
If the number of male children is more than 1 and there is at least one female child, we link the last male child to the first female child.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if (!female_idx.empty())
{
if (male_idx.size() > 1)
{
family[male_idx.back()].sibling = &family[female_idx[0]];
}
if (female_idx.size() > 1)
{
for (int i = 0; i < female_idx.size()-1; ++i)
{
family[female_idx[i]].sibling = &family[female_idx[i+1]];
}
}
}
C++ Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
struct Details
{
std::string name;
std::string parent_name;
int birth; // year of birth
std::string death;
std::string religion;
std::string gender;
int index;
bool has_child = false;
bool processed = false;
Details * parent;
Details * sibling;
Details * first_child;
Details(){}
Details(std::string name_, std::string parent_name_, int birth_, std::string death_, std::string religion_, std::string gender_, int index_):
name(name_), parent_name(parent_name_), birth(birth_), death(death_), religion(religion_),
gender(gender_), index(index_), parent(nullptr), sibling(nullptr), first_child(nullptr) {}
};
void map_siblings(std::vector<int> & male_idx, std::vector<int> & female_idx, std::vector<Details>& family, int curr_ruler_idx)
{
if (!male_idx.empty())
{
family[curr_ruler_idx].first_child = &family[male_idx[0]];
if (male_idx.size() == 1)
{
if (!female_idx.empty())
{
family[male_idx[0]].sibling = &family[female_idx[0]];
}
}
else
{
for (int i = 0; i < male_idx.size()-1; ++i)
{
family[male_idx[i]].sibling = &family[male_idx[i+1]];
}
}
}
else
{
family[curr_ruler_idx].first_child = &family[female_idx[0]];
}
if (!female_idx.empty())
{
if (male_idx.size() > 1)
{
family[male_idx.back()].sibling = &family[female_idx[0]];
}
if (female_idx.size() > 1)
{
for (int i = 0; i < female_idx.size()-1; ++i)
{
family[female_idx[i]].sibling = &family[female_idx[i+1]];
}
}
}
}
void map_parent_children(std::vector<Details>& family, int curr_ruler_idx)
{
std::vector<int> next_gen_m_idx; // stores index of male members of next generation
std::vector<int> next_gen_f_idx; // stores index of female members of next generation
for (int i = 0; i < family.size(); ++i)
{
if (family[i].parent_name == family[curr_ruler_idx].name)
{
family[curr_ruler_idx].has_child = true;
family[i].parent = &family[curr_ruler_idx]; // mapping parent
if (family[i].gender == "M")
{
next_gen_m_idx.push_back(i);
}
else
{
next_gen_f_idx.push_back(i);
}
}
}
//sort both vectors according to age
if (family[curr_ruler_idx].has_child)
{
static const auto by_age = [family](const int i, const int j)
{
return family[i].birth < family[j].birth; // year of birth is smaller means age is bigger
};
std::sort(next_gen_m_idx.begin(), next_gen_m_idx.begin(), by_age);
std::sort(next_gen_f_idx.begin(), next_gen_f_idx.begin(), by_age);
map_siblings(next_gen_m_idx, next_gen_f_idx, family, curr_ruler_idx);
}
}
std::vector<std::string> order_of_succession(std::vector<Details>& family, int first_ruler_idx)
{
std::vector<std::string> rulers;
int curr_ruler_idx = first_ruler_idx;
map_parent_children(family, first_ruler_idx);
while (true)
{
if (family[curr_ruler_idx].death == "-" &&
family[curr_ruler_idx].religion != "Catholic" && !family[curr_ruler_idx].processed)
{
rulers.push_back(family[curr_ruler_idx].name);
}
family[curr_ruler_idx].processed = true;
if (family[curr_ruler_idx].has_child)
{
curr_ruler_idx = family[curr_ruler_idx].first_child->index;
}
else
{
if (family[curr_ruler_idx].sibling != nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].sibling->index;
}
else
{
while (curr_ruler_idx != first_ruler_idx &&
family[curr_ruler_idx].parent->sibling == nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].parent->index;
}
if (curr_ruler_idx == first_ruler_idx)
{
break;
}
if (family[curr_ruler_idx].parent->sibling != nullptr)
{
curr_ruler_idx = family[curr_ruler_idx].parent->sibling->index;
}
}
}
map_parent_children(family, curr_ruler_idx);
}
return rulers;
}
int main()
{
int n;
std::cin >> n; std::cin.ignore();
std::vector<Details> family_details;
int first_ruler_idx;
for (int i = 0; i < n; i++)
{
std::string name;
std::string parent;
int birth;
std::string death;
std::string religion;
std::string gender;
std::cin >> name >> parent >> birth >> death >> religion >> gender; std::cin.ignore();
if (parent == "-")
{
first_ruler_idx = i;
}
family_details.push_back( Details(name, parent, birth, death, religion, gender, i));
}
std::vector<std::string> ruler_order = order_of_succession(family_details, first_ruler_idx);
for (int i = 0; i < ruler_order.size(); ++i)
{
std::cout << ruler_order[i] << "\n";
}
}
Note : One test case is not passed
Check out this on Github
If you have a different solution for finding orDer oF succeSsion, please share it in the comments below.
Other Competitive Programming Problems and Solutions
Stock Exchange Losses - CodinGame
Dungeons and Maps - CodinGame